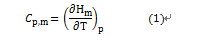因特尔是世界上最大的芯片制造商之一,这个大家都知道,你的电脑用的很有可能就是因特尔的处理器。
因特尔处理器是性能优良的代名词,但是,因特尔也有一段不堪的往事。这件事还和一个神秘的常数,以及一个困扰人类2300多年的神秘数学猜想有关。
1994年,因特尔推出了奔腾处理器,这是当时市面上最先进的处理器之一。但是好死不死,这个世界上最坚硬的盾,遇到了最锋利的矛——能逼疯计算机的数学家。
 出了bug的奔腾处理器
@wikipedia
出了bug的奔腾处理器
@wikipedia
这不难理解,因为数学家需要处理数学问题。尤其是当他们不知道怎么证明一个猜想的时候,他们就会用暴力穷举的方法。
在这个过程中,计算机就会被逼到绝境。每次一有先进计算机出现,数学家们就会摩拳擦掌,饿虎扑食一般把先进计算机团团围住。加拿大西蒙弗雷泽大学(Simon Fraser University)的数学家 Peter Borwein 曾经对《科学》表示,通过让计算机不断进行简单重复的计算,计算机的计算能力“就会到达崩溃的边缘”,开始出错,类似于还有1分钟就要交卷的学生仔。

这次,奔腾也没有逃脱数学家的魔爪。把奔腾逼到崩溃DAN疼的,是一个叫做布朗常数(Brun’s constant)的神秘常数。
布朗常数和质数有关,而且表达式很简单,小学生也能看懂——

可是布朗常数是干哈用的呢?这里面的数字又是啥呢?
这就要和把数学家们逼疯的著名猜想——孪生素数猜想讲起了。
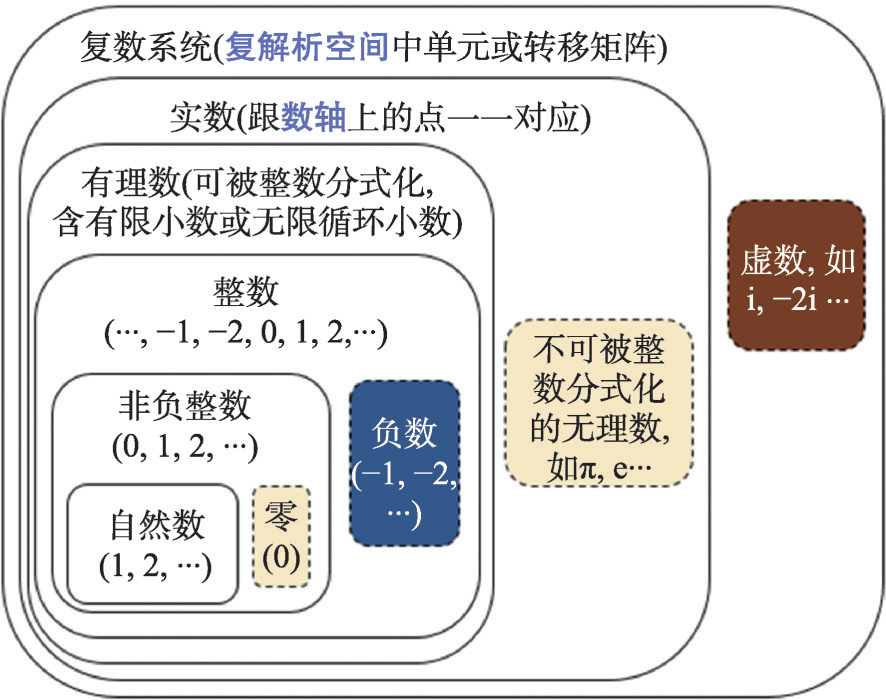
欧几里得在《几何原本》里已经证明存在无穷多的质数。数学家们也知道,如果从1开始一直数下去的话,一开始质数出现的频率比较高,后来就变得比较珍稀了。
比如,两位数里有23%是质数,但是十位数里只有4%是质数,而百位数里,质数只占1%不到。
不过,质数还有一个奇特的现象,那就是虽然质数的分布变得越来越稀疏,但是两个连续质数之间的距离却似乎不会增长,比如3和5差2,41和43也差2,101和103也差2,10007和10009也差2。
这样相差2的一对连续质数就被叫做孪生素数,也叫孪生质数。
 100以内的质数(黄底)和孪生质数(红色)
100以内的质数(黄底)和孪生质数(红色)
2300年前,欧几里得就开始大胆脑补了,会不会孪生质数有无穷多对呢?一定是这样的嗯。然后大家为了纪念欧几里得的脑洞,就把它叫做孪生素数猜想。
这个猜想也变成了一座让数学家闻风丧胆的数学金杯。
比如,在1912年的国际数学家大会(ICM)上,德国数学家 Edmund Landau 就举出了当时数学界觉得不可能解决的4个猜想,其中之一就是孪生素数猜想。这4个问题后来就被叫做兰道问题。
100多年后的今天,这4个兰道问题还是猜想。
 挪威数学家 Viggo Brun
@wikipedia
挪威数学家 Viggo Brun
@wikipedia
不过在1919年,毛发浓郁的挪威数学家 Viggo Brun 有了个大突破。Brun 证明,就算有无穷多对孪生质数,它们的倒数的和,也就是

会收敛于一个有限的值,就好像1/2 + 1/4 …最后等于1一样。

这个常数,就被叫做布朗常数。
 布朗常数收敛于一个有限值
@wikipedia
布朗常数收敛于一个有限值
@wikipedia
其实,布朗常数对于数学家们来说是一个精神打击。因为如果 Brun 证明孪生素数的倒数和不收敛,是发散的,这就等于宣布,孪生素数有无穷多对,那么孪生素数猜想就得到了证明,欧几里得挖的坑就可以填上了。
而存在布朗常数,等于说孪生素数问题还是没有得到证明,只不过现在大家知道孪生素数的分布确实很稀疏,但我们还是不知道孪生素数是不是有无穷多对。
另外,虽然 Brun 能证明布朗常数存在,但并不能计算出它的每一位,就像我们还无法计算派的小数点后的每一位数字一样。不过和派不一样,我们直到现在也不知道布朗常数是不是无理数。如果能多算出几位它小数点后的数字,我们或许就能了解它到底是什么品种的妖怪了,因此许许多多的数学家开始计算布朗常数。
随着计算机的出现,数学家们想到了用暴力硬算的方法解决这个问题。
1974年,为美国海军干活的两个数学家 Daniel Shanks 和 John Wrench Jr 报告了用计算机暴力算出来的布朗常数,他们让悲催的计算机穷举了2百万个质数。
2年后,澳大利亚国立大学的数学家 Richard Brent 更加暴力,他让计算机穷举了224 376 048对孪生质数,利用这些质数,他算到布朗常数的小数点后第8位,得到1.90216054。

顺说一句,2011年谷歌竞拍加拿大北电网路(Nortel Networks)的无线专利技术的时候,出的价就是1,902,160,540美金。数学家们看到 Brent 这种勇士,好长一段时间都不说话了,因此布朗常数的故事就风平浪静了一大会儿。接着到了90年代,因特尔就萌萌哒推出了最强处理器。
美国弗吉尼亚州的林奇堡学院(Lynchburg College)的数学家托马斯· 小火车好好地(Thomas Nicely)看到因特尔处理器很心动啊,他早就想算一把布朗常数了,毕竟当时也没有矿币可以挖。

他打算磨死计算机,让它算到万亿。
因为知道数学家都是计算机杀手,为了确保计算机不会崩溃搞事情,他还用了双保险——用2种方法计算。
这俩方法的差异差不多等同于,算1/3+1/7的时候,用0.33+0.14=0.47这个方法,或者1/3 + 1/7 = 10/21 = 0.48这个方法。照理来说算出来的结果差距应该不大。
但是呢,Nicely 用这两个方法得到的结果一比之后,却发现差距比欧几里得的脑洞还大。
用排除法一波debug以后,Nicely 发现问题的关键在于2个质数,那就是824 633 702 441和824 63 702 443,它们的倒数的小数点后的第10位被算错了。
但是,Nicely 不确定这个问题是计算机硬件的问题,还是软件的问题,总之不是他的问题。于是他让因特尔古早处理器486又算了一次,结果486倒是算对了。
4个月后,Nicely 又用其他两台装有奔腾的计算机做了一次计算,这个问题又出现了。
很明显,这是因特尔奔腾的硬件有毛病。Nicely 估计,这个处理器大概会把10亿个倒数里的1个算错。因为要算布朗常数,计算机就要计算数十亿的倒数,因此出错在所难免。
Nicely 很快联系了因特尔,要求一起写数论作业看看是怎么回事,不过因特尔不是很热情,他们要小明出去。

Nicely 觉得很无语,于是就在11月把这件事的前因后果写了邮件,群发给了小伙伴们。
这件事很快就被美国有线电视新闻网(CNN)等媒体报道。奔腾算倒数时会偶发智障的事件被公开后,因特尔就不得不召回旧的处理器并为用户更换新的。
后来因特尔承认,其实他们在生产奔腾的时候就知道这个问题了,但是计算了一波后他们发现,90亿用户里,只有1个会受到影响,因此一开始没有召回。就是“我是错了,但是我还是比别人先知道我错了”的意思。

当时因特尔已经卖掉了一百多万台装有奔腾处理器的计算机,所以1995年1月17日,因特尔宣布,因为这次召回事件,他们损失了4.75亿美金(相当于现在的8.23亿美金,58亿人民币,58个小目标)。
这个问题,史称奔腾浮点除错误(Pentium FDIV bug),被写入了维基词条,是因特尔最想让大家遗忘的黑历史之一。
那么,为什么奔腾奔腾会算错呢?问题出在它做除法的时候。
原来,因特尔做了一个查找表,也即是类似于三角函数表这样的方便计算的表格,这样不用每次都亲自算一遍,查一下表格可能会更方便。但是这个查找表漏了5个数据,导致做除法的时候有一定的几率犯错。
瑞士洛桑联邦理工学院加密算法实验室的教授 Arjen Lenstra 还给因特尔补了一刀:“我们数学家早就知道数论对计算很有用啦。在卖处理器之前好好算一下数论的东西嘛真是的。”

对了,后来在2002年,不隶属于任何已知大学或组织的法国浪人数学家 Pascal Sebah 又更新了布朗常数——1.902160583104。
而在2013年,孪生素数猜想也有了一个大突破——华人数学家张益唐在58岁时发表关于孪生素数猜想的重要论文,证明了相差小于7000万的素数对有无穷多对。
 张益唐
张益唐
如何证明我比计算机厉害?
( •_•)
数学老师教出数学家,数学家能逼疯计算机,我能逼疯数学老师,所以我比计算机厉害,Q.E.D.